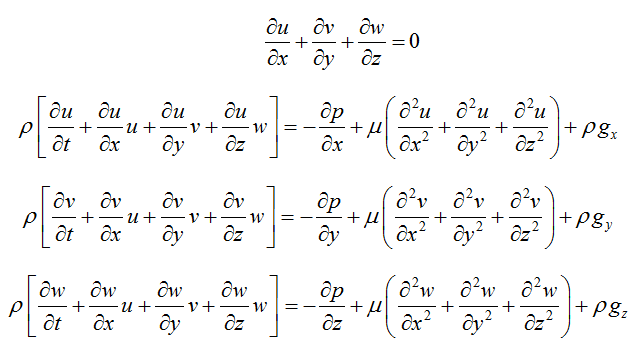Lifting-line model of a finite-span wing (Wingtip vortices)

This blog is meant to give a basic definition about the wingtip vortices and to give a sense of the lifting-line model of a finite-span wing.

Tip vortices and down-wash generated behind an airplane are shown.

You may see on the pictures the tip vortices that are visualized by the clouds. On the second picture, there's a plane shortly after take-off, very high angle of attach, so there is a very huge lifting force of course, and you can see the vortices generated and their mixing in the air with the upstream and downstream flows.

Another picture of an agriculture airplane of which's tip vortex is visualized. Significant is the size of the vortex and its huge intensity, compared to the size of the aircraft.

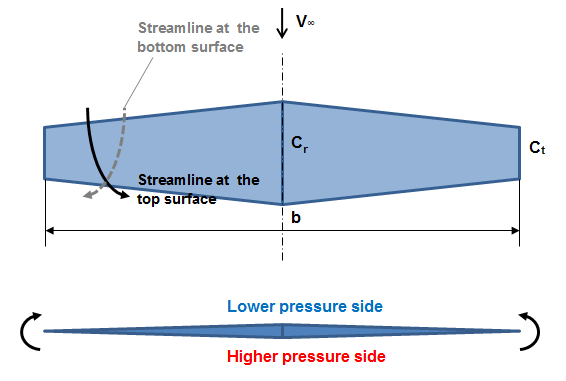
The following figure is showing the visualization of flow past a rectangular wing. Due to the pressure difference between the upper part and the lower part and the fact that the wing has a finite span, there will be a certain tendency of the air to flow from the higher pressure to the lower pressure part. We have counter rotation vortices at the ends of the wing. If I have a streamline at the bottom surface then near the wing tip it’ll be deflected as it’s indicted with the dashed line. On the other side, on the suction side, the streamlines will be deflected towards the fuselage.

Initially it was very difficult to create a realistic geometric model of this type of the vertical wake so they came up with an idea; instead of taking this spiral folding, make our “vortical” wake behind the airfoil completely flat. It doesn’t mean that there will be no vorticity. It means that the self-induction is completely neglected and the vertical flow is assumed to be completely flat. It’s of course not true but we can build the model of the wing.

Flow past a wing is modeled by the superposition of the uniform free stream and the velocity induced by a plane vortex sheet “pretending” to be the cortex wave behind the wing.

The idea of Prandtl was that; imagine if we have infinitely many vortex lines, of which each of them has such shape as shown on the figure:

(It extends from infinity along what is called a lifting line, which completely replaces the wing and goes back to infinity.) These infinitely many vortex lines are overlapping along the lifting line. Beyond the lifting line they form a vortex sheet which is a flow-stream with distributed vorticity. Where they overlap, they create an infinitesimal contribution to "gamma" – dГ, to the total vorticity – Г(y). Since they overlap, Г will have a symmetrical distribution. Each of these lines is called a horseshoe vortex.

Rohács József, Gausz - BME - Aerodinamika page 78.Figure 4.4.

In other words, the vortex sheet behind the wing is “woven” from continuum of infinitesimally weak horseshoe vortices. These vortices are “attached” to the lifting line leading to a continuous distribution of circulation along the wing span.

We’d like to calculate the velocity, induced by this vortex sheet along these lines. Each of these horseshoe vortices induces a certain velocity distribution along y line, which is completely vertical, which means that higher velocity is in z direction. Next it is assumed that each infinitely thin slice of the wing generates the (differential) contribution to the total aerodynamic force as it were a 2D airfoil. Each slice “senses” its individual direction of “free stream”, which results from the real free stream vector V_∞ and the vertical (normal to the vortex sheet) velocity induces at the lifting line in the point corresponding to the position of the wing slice.

References:

Photos: Airliners.net, NASA.gov

• Timo Harsch - Airbus A340-642 ZS-SNG

• Colin Hollywood Photography - Boeing 777-F6N B-2083

• Helmut Schnichels - Airbus A380-842 VH-OQA 

• Aerodynamics lecture, by Jacek Szumbarski, Warsaw University of Technology

• Rohács József, Gausz - BME - Aerodinamika jegyzet, page 78. figure 4.4.

Navier-Stokes equation for 3D compressible and incompressible flows

In this blog I would like to present the general form of the Navier-Stokes equation for both incompressible and compressible flows. As in most textbooks you may not find the fully expanded forms in 3D, here you have them all collected. For the first look, it might scare you but after breaking it down, it’s all simple. 

Incompressible flow:

• Frame invariant form:

• Dimensional form:

The subscripts imply differentiation with respect to the variables. Primes (‘) indicate that the unknowns are dimensional. The system of equations are solvable, since there are 4 equations and 4 unknowns: 

Fully expanded form to 3D coordinates:

Compressible flow:

• Frame invariant form:

• Fully expanded form to 3D coordinates:

Resource:

• Aerodynamics for Engineering Students, Sixth Edition, E.L. Houghton, (etc.)

The equations were typed into Microsoft Office, unfortunately blogger.com does not have a possibility to type equations so I had to make screenshots of them. You may use them freely as you wish. Beware of the fact that there might be minor mistakes in the formulas, although I checked them several times.

Engineering approach to prediction of the laminar-turbulent transition in the boundary layer (e^N method)

The most popular and effective engineering methods of transition predictions are based on the idea of the e^N method.

Since the amplification is of the exponential form, the corresponding amplification factor with distribution of x will look like as given on the Figure. Note that starting from the maximum point, this Tollmien-Schlichting wave is not amplified anymore and it starts to be diminishing. But this is just one frequency. If I choose any other frequency, I can have such lines that’ll rise later. We have infinite number of Tollmien-Schlichting waves with different frequencies and we have individual curve of each of them.

The idea of e^N method for transition prediction was published by Van Ingen in 1956.

The above formula describes the cumulative amplitude growth that is determined for a bunch of modes with different frequencies. One can obtain as a result a family of lines, showing how the amplification factor of each mode grows downstream the boundary layer (BL). In principle, if I have a boundary layer, then in BL we have an excitation of all possible frequencies. Then, one can define the envelope for this family, which is a line effectively parametrized by the frequency. (see Figure) 

We assume that the actual amplification of disturbances in the BL will be inside this envelope. So if I choose a line, which sort of has all this infinitely many lines underneath, then I will be on the same side. So if I can calculate this envelope line, which goes on the top of all individual lines, I’ll have sort of a border of a maximum possible local amplification that may in principle happen in any cross section on the TBL. The hypothesis behind it also says that the actual transition point will be when this envelope will reach a certain value of this logarithm. For example, when the flow is in a very calm atmosphere, where the lever of turbulence outside the BL is very-very small, then the BL will survive without being stabilized such amplification and a local amplification up to say 9 orders of magnitude of initial disturbance. So this logarithm is 9.

But if the external disturbance field will be much higher, then that means that from the very beginning the disturbances are large, so it’s enough e.g. to amplify them by 4^th order of magnitude, or maybe 5^th order of magnitude, before they actually cause a transition to the TBL.

Physically the idea is primitive but surprisingly it works very well. Over the years, people gained a huge experience in manipulating this amplification factor and e.g. those Aerodynamists who use for aerodynamic design software like Xfoil, they know very well which amplification factor with this e^N criterion to choose. Dependently on the different conditions for which this or another airfoil is actually designed. If it’s designed for a glider, which supposed to fly in a very calm atmosphere, that’s the situation it supposed to get its best of its performance, then the one should choose this very-very small. The level of this is not about the level of external atmosphere but it’s also about the quality of the surface of the wing. If it’s very well polished, like a “glass”, which is most typical for modern gliders then this number can reach ever 11, for the measure of transition. But if we have something like a small wind turbine, small like, someone puts it on a farm, there is send around, there are insects on it, probably bird was hit by the blade, there is feather here and there on it, so the quality is very-very bad, it could be even lowered to around 4, especially if this contamination of the surface is close to the leading edge.

There is another important issue. If you have an airfoil and you’re worrying about making it dirty, then if this dirtiness is in front, near the leading edge, it’s really dangerous. If it’s far away, near the trailing edge, it’s not dangerous. This is pretty obvious. Initially the thickness of the BL is very-very small, meaning that even a small obstacle from the point of view of the laminar BL is huge. The same obstacle, when flown to the airfoil somewhere near the trailing edge, for the BL which is now 10 times thicker, is simply less sensitive.

Reference:

• Aerodynamics lecture, by Jacek Szumbarski, Warsaw University of Technology

Changes of the slope of the lifting force characteristic CL=CL(α)

How the slope of the lifting force characteristic C_L = C_L (α) changes with increasing thickness and camber of the airfoil according to the potential flow theory and according to the thin airfoil theory?

Potential flow theory:

According to the potential flow theory, the slope of the lift force characteristic for the Joukovsky’s non-symmetrical airfoil with zero thickness (ε = 0) is expressed by the approximate formula:

where f is the camber ratio (ratio between the maximal deflection of the mean camber line and the chord of the airfoil).

The small correction is proportional to the square of the camber. The thicker the profile of the airfoil, the more the slope of C_L = C_L (α) is increased.

The formula for the lift force coefficient can be written as follows:

where β is negative and corresponds to zero lift condition.

The deflection of the airfoil (AoA) leads to the vertical shift in the characteristic C_L = C_L (α) curve, as the equation is α dependent.

Thin airfoil theory:

The slope of the lift force characteristic C_L = C_L (α) is equal:

From which it can be clearly seen that the slope does not depend on the airfoil camber. It does not include also the correction as it was in the potential flow theory.

The formula for the lift force coefficient can be written as follows:

where

 is the negative angle of attack at which the camber airfoil is not producing any lift.

Summarizing it: